光槓桿（Optical Lever）原理

光槓桿（Optical Lever）原理
國立臺灣師範大學物理系李聖尉碩士生/國立臺灣師範大學物理系蔡志申教授責任編輯

此為一簡單的裝置，卻可有特殊不同之結果。如同只要有一根棍子及一顆石頭，即可有如同大力士把重物舉起的驚人之舉！

首先，只考慮如下圖一之圖形，而忽略數學的部份：

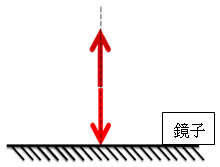
圖中底端為鏡子，虛線為法線。當我們從法線入射一束光線（亮紅箭號），即入射角為 $$0^\circ$$，此時反射角亦在法線上（暗紅箭號）。

再如下圖：

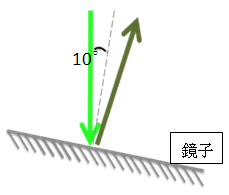
圖二類似上圖，此時為斜向入射，入射角為 $$10^\circ$$ 則反射角亦為 $$10^\circ$$。

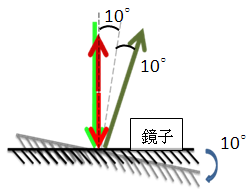
但如果把兩圖疊合如圖三

如同僅把圖一之鏡子順時針旋轉 $$10^\circ$$，其餘不變。此時入射角及反射角亦皆為 $$10^\circ$$，且入射角與反射角之間的夾角為 $$20^\circ$$。整理以上之情況：當鏡子旋轉 $$10^\circ$$ 時，則入射角與反射角之間的夾角為 $$20^\circ$$ 兩者相差兩倍。由於 $$10^\circ$$ 為我們任意假設，因此可推論在任何角度下亦皆可成立，即：

當鏡子旋轉 $$\theta$$ 角，則入射角與反射角之間的夾角為（$$2\theta$$）角

以上即為光槓桿（Optical Lever）原理。

接下來，我們從嚴謹的角度來証明光槓桿原理：

由於圖形稍嫌複雜，所以我們先依序在各線條上編上編號 －

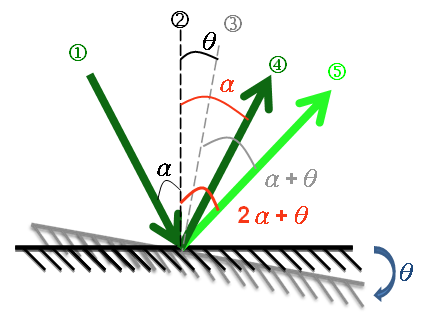
圖中部份如前面所看到的圖形，黑色組為原本鏡面/法線組；灰色組為後來的鏡面/法線組，兩者相差 $$\theta$$ 角。1 / 4 分別為打在黑色鏡面上的入射/反射光；  1 / 5 分別為打在灰色鏡面上的入射/反射光。（兩者入射光皆為同一條）

在此我們如上想要探討旋轉前後的反射光線之夾角（亦即編號  4 、 5 的夾角）。

Ⅰ、因為鏡面旋轉前後夾 $$\theta$$ 角，又法線各自與鏡面夾 $$90^\circ$$ 角，因此 2 及 3 夾 $$\theta$$ 角
Ⅱ、設原鏡面上的入射角為 $$\alpha$$ 角，則反射角（2 及 4 之夾角）亦為 $$\alpha$$ 角
Ⅲ、則灰色鏡面組之入射角（1 及 3 之夾角）為 $$(\alpha+\theta)$$ 角；反射角（3 及 5 之夾角）亦為 $$(\alpha+\theta)$$ 角。
Ⅳ、此時，我們想要的答案

$$=$$ 旋轉前後的反射光線之夾角
$$=$$ 4、5 的夾角
$$=$$ 圖中兩紅色弧角相減
$$=$$〔弧角（2 5）〕$$-$$ 弧角（2 4）
$$=$$〔弧角（2 3）$$+$$ 弧角（3 5）〕$$-$$ 弧角（2 4）
$$=[(\alpha+\theta)+\theta]-\alpha$$
$$=2\theta$$

由此可知，結果和上述方法一致：

當鏡子旋轉 $$\theta$$ 角，則入射角與反射角之間的夾角為 $$(2\theta)$$ 角

另外，值得一提的是，有一式子：$$S$$（弧長）$$=r$$（半徑）$$\times\theta$$（夾角）
因此當我們把距離 $$(r)$$ 拉遠，再配上光槓桿原理，便可輕易測出微小的弧長變化。

此原理雖然簡單，卻在光學等其餘地方皆有廣泛的應用。以下簡單列舉二項有名的例子 －卡文迪西（Henry Cavendish, 1731-1810）實驗、原子力顯微鏡（Atomic Force Microscope，AFM）。

卡文迪西（Henry Cavendish, 1731-1810）實驗

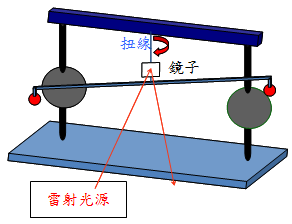
如圖。此實驗利用到扭擺裝置；由於球與球之間受萬有引力吸引而使中間的扭線受到扭轉，再利用光槓桿原理^〔註一〕，因此就算小角度也可量測出微小之萬有引力常數 $$(G=6.67\times 10^{-11}~N\cdot m^2/kg^2)$$。

另外值得一提的是－現今重作此實驗當然會選用直準性高的電射當作光源。但在 18 世紀的當時，卡文迪西在沒有雷射光源的情況下完成此實驗是值得令人敬佩的。

註一：雷射光源打在固定在扭線上的小面鏡子，因光槓桿原理使得反射光線的偏轉角度會放大兩倍，以利於測量。

原子力顯微鏡（Atomic Force Microscope，AFM）

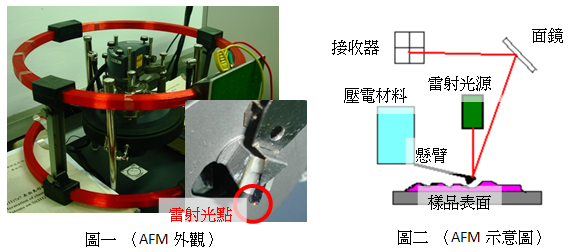
此儀器（圖一），可看到物質表面的結構，其示意圖如圖二（詳細原理由於篇幅故略）。圖三、圖四為實際偵測所掃描出來之圖片。唯圖四下半部另有經電腦模擬而得到之３Ｄ立體圖形。

圖二、圖三：慈濟大學醫學系 劉哲文教授提供

圖四：Liou et al. 2002. Biochemistry. 41:8535-9.