RL電路
RL電路(RL Circuit)
加州大學柏克萊分校物理系 2012 盧奕銓
- 定義及基本概念
一個電路中,如果「被動元件(不會自己提供能量)」只用了電阻器 \(R\) 和電感器 \(L\),而沒有用到電容器 \(C\),這樣的電路就稱為 \(RL\) 電路。電路中可以有電池、電流源等其他「主動元件(會自己提供能量)」,並不一定只能有電阻器和電感器。最基本的電感器是由線圈所組成,當通過電感器的電流改變時,通過線圈的磁通量會跟著改變。由法拉第定律可知,電感器本身會產生感應電動勢,試圖阻止磁通量改變。因此,通過電感器的電流,會和驅動電流的外力不同步,而造成 \(RL\) 電路中許多特殊的現象。
- RL直流電路
如果流過線圈(電感器)的電流變化不太快,那麼通過線圈的磁通量 \(\Phi\) 會和電流 \(I\) 成正比:\(\Phi=LI\),其比例常數 \(L\) 就定義為這個線圈的「電感」。
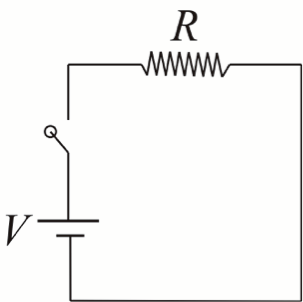
法拉第定律說明,如果電流改變,電感器就會產生感應電動勢 \(\epsilon=-d\Phi/dt\),這樣的電動勢就像一個虛擬電池,存在線圈內部,試圖阻止電流和磁通量的改變。以下是一個簡單的例子:如圖一(a),假設一個迴路中只有一個直流電池 \(V\)、一個電阻器 \(R\) 和一個開關,在開關接通之前,通過整個迴路的電流很明顯是零;而當開關接通之後,由歐姆定律知,電池會馬上送出一個大小為 \(V/R\) 的電流,流過電阻器之後,順著電路流回至電池本身。
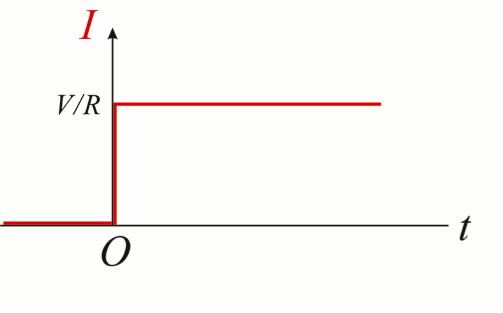
所以,如果我們畫出電流 \(I\) 與時間 \(t\) 的關係圖,將會是圖一(b) 的樣子,其中 \(t=0\) 是開關接通的時刻。注意電流在 \(t=0\) 時,是直接從 \(0\) 跳至 \(V/R\)。
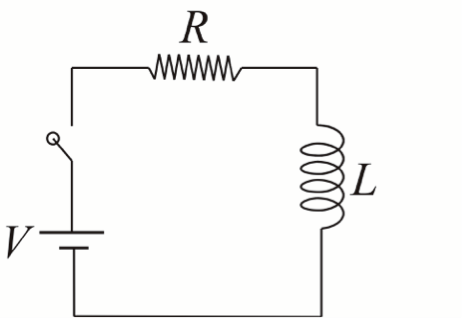
現在,如果電路中裝有電感器 \(L\),如圖二(a),在開關尚未接通之前,電流當然還是零;而當開關接通的那一剎挪,電池一樣想要將電流送出去,但因為電感器會偵測到,電池想送過來的電流有增加磁通量的趨勢。
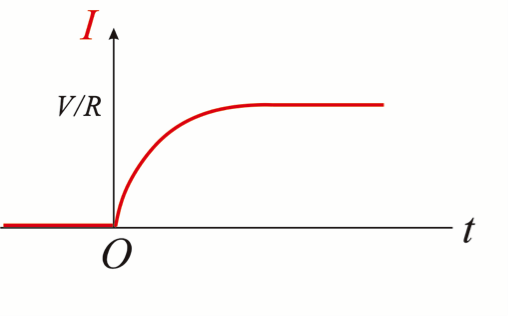
於是,電感器馬上產生感應電動勢 \(\epsilon=-L(dI/dt)\) 來阻止這樣的電流,因此,通過整個迴路的電流,沒有辦法像之前一樣,數值一下子就從 \(0\) 跳到 \(V/R\),而是會從 \(0\) 慢慢地連續變化成 \(V/R\),如圖二(b) 所示。這是電感器一個很重要的功能:電感器在電路改變的瞬間(像是接通開關),具有保持原有電流數值(在這個例子裡是 \(0\))的能力。
用不嚴謹的數學也可以解釋上面第二個例子。當開關接通後,在電感器存在的情況下,假設電流還是可以直接從 \(0\) 跳至 \(V/R\),如圖一(b)所示,電流在 \(t=0\) 處有一個不連續的斷點,那麼電流曲線在 \(t=0\) 處的斜率是無限大。
所以電感器在這瞬間所產生的感應電動勢將會是 \(\epsilon=-L(dI/dt)=\infty\),表示電感器電壓已經大到可以反過頭去幫電池充電了,很明顯不合理。所以,若要讓感應電動勢的數值是有限的,唯一的可能就是,電流必須要處處連續,而不可以有任何斷點。這就是為什麼在有電感器之後,電流曲線只會像圖二(b)那樣,慢慢地上升。
- RL交流電路
如果電路中所接的電池是交流電源,那又會有更多現象產生。當開關剛接通時,也會有上述電流遲緩的現象,但是如果我們等待一段時間之後,這遲緩現象就會消失。數學上,這種短暫就消失的行為稱為暫態(transient term)。至於暫態消失後,電路會如何運作,則視電路組態而定。我們不妨考慮以下簡單的電路:一個交流電池 \(V\)、開關、電阻器 \(R\)、電感器 \(L\) 串聯在一起。前面提到,電感器本身的電壓是 \(-L(dI/dt)\),所以由柯希荷夫定律知,
\(\displaystyle V-IR-L\frac{dI}{dt}=0\)
其中我們假設交流電是個正弦波 \(V=V_0\sin{(\omega t)}\),\(V_0\) 是交流電的振幅。解這道方程式最常見的方法是,先把 \(V\)「複數化」,我們令 \(V=V_0e^{i\omega t}\),但真正的電源其實是 \(V\) 的虛部。再來,當電源接通之後,假設我們等待夠久,暫態現象消失之後,我們預期電流也會像電池般有週期性,所以我們可以猜「複數化」後的電流可以寫成 \(I=I_0e^{i\omega t}\) ,其中 \(I_0\) 是電流的振幅。將 \(V\) 及 \(I\) 代入方程式中,並消去 \(e^{i\omega t}\) 之後,得到
\(V_0-I_0R-I_0i\omega L=0\)
這道方程式可以解讀成:一個直流電源 \(V_0\) 驅動了電流 \(I_0\),經過電阻器時,電壓下降了 \(I_0R\),而經過電感器時,電壓下降了 \(i\omega LI_0\)。由於 \(R\) 是電阻器的電阻,我們也可以定義 \(i\omega L\) 是電感器的某種電阻,習慣上稱之為「阻抗」。對於任何複雜的交流電路問題,都可以將電感器想像成具有 \(i\omega L\) 阻抗的電阻器,而電阻器的串、並聯公式都可以直接套用在電感器上。在本例中,電阻器因為和電感器串聯,等效阻抗就是 \(R+i\omega L\),所以由歐姆定律可以馬上寫下:
\(\displaystyle I_0=\frac{V_0}{R+i\omega L}\)
至此,我們已經解完方程式了,而真正的電流就是 \(I=I_0e^{i\omega t}\) 的虛部:
\(\displaystyle I=\text{Im}(\frac{V_0}{R+i\omega L}e^{i\omega t})=\frac{V_0}{\sqrt{R^2+(\omega L)^2}}\sin{(\omega t-\phi)}\)
其中 \(\phi=\tan^{-1}(\frac{\omega L}{R})\)
所以電流本身跟外加電源一樣是個正弦波,但是它和電源並沒有完全同步,而是相差了一個相角 \(\phi\)。而電流的振福也與電阻、電感、以及交流電的頻率有關。
參考文獻
- Wolfson, R. Essential University Physics (2011), 2nd edition. Addison-Wesley.


 前一篇文章
前一篇文章 下一篇文章
下一篇文章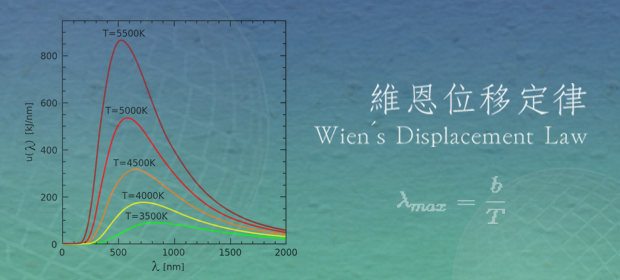 維恩位移定律
維恩位移定律 
