電路系統的線性獨立特性（Linearly Independent of Circuitry）

電路系統的線性獨立特性（Linearly Independent of Circuitry）
國立台灣師範大學附屬高級中學物理科陳智勝老師/國立臺灣師範大學物理系蔡志申教授責任編輯

一般的電路分析，我們可以利用等效電阻公式將線路化簡，其中 n 個電阻的串連線路其總電阻為 。 n 個電阻的並聯線路其總電阻為 。再利用歐姆定律 V = IR（V 為電阻兩端的電壓， I 為流經電阻之電流， R 為電阻）即可得到線路各處之電流量值，與各電阻兩端的電壓值。

若是處理較複雜的電路，則可以利用克希何夫定律（Kirchhoff circuit laws）來加以分析。其中克希何夫電路定律的兩大定則為： 1. 任一節點流進的電流值等於流出的電流值。 2. 任一迴路的電位變化為零。這兩大定則分別為電荷守恆與能量守恆的必然結果。

例如有一電路如下所示：

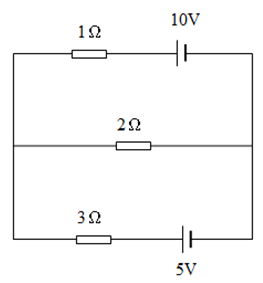若想知道流經 2Ω 電阻的電流為何，一般的解題方式為利用克希何夫定律來分析。

解題方式如下：首先必須假設各線路的淨電流如下圖所示。

然後再根據克希何夫定律列出相關方程式：
      1. 任一節點流進的電流量值等於流出的電流量值。
                I₁ = I₂ + I₃
      2. 任一迴路的電位變化為零。
                10 － I₁ × 1 － I₂ × 2 = 0
                5 ＋ I₃ × 3 － I₂ × 2 = 0
將三式解聯立方程式，即可得到流經2Ω電阻的電流值為 I₂ = 35/11 (A)

除此之外，我們打算利用電路的線性獨立性，來解出 I₂ 。方式如下：
首先，我們先將線路取走 5V 電池，只留下 10V 的電池，如下圖所示。如此一來電路便大幅簡化，變成一般串並聯的電路。

如此利用等效電阻以及歐姆定律，即可計算出此時的流經 2Ω 電阻的電流值為 I_a = 30/11 (A)

其次，將原電路中的 10V 電池取走，只留下 5V 電池，變成如下圖所示。

上述的動作即是分別計算 10V 和 5V 電池對於 2Ω 電阻的電流貢獻，分別是 I_a 與 I_b 。此時我們發現 I_a ＋ I_b 的值即可得到 I₂。

值得注意的是，在計算的過程之中，我們並無利用複雜的電路分析、解聯立方程式，亦可得到和克希何夫定律分析出來的結果相同。這樣的分析方式確實是一個可行的解題方法，而且其優點在於可以避免繁瑣的計算過程，即可得出複雜線路中的電流值。

探究其原因在於電阻器是一種線性元件，即電阻器上若加上 V₁ 電壓，對應得到 V₁電流；若加上 2V₁電壓，則所得的電流也是倍增為 2V₁ 。因此電路中的電動勢對於電阻的電流貢獻是獨立的。故我們分別計算兩個電動勢對於電路上電阻的電流貢獻，再線性相加其值，即可得到總電動勢對於該電阻的電流貢獻。

參考資料：
1.維基百科–克希何夫電路定律  http://en.wikipedia.org/wiki/Kirchhoff%27s_circuit_laws