漂移速度

漂移速度 (Drift Velocity)
國立臺灣大學電信所電波組碩士班 林庭毅

我們經常會聽到人家這麼說：電流是正電荷移動所造成的。

或者你想要嚴格一點，告訴大家正電荷不會移動，是電子在動，但是對於一個物理議題的探討而言，如何等效兩個問題並解決其中一種是比較重要的事情，因此今天我們還是先內建這樣的想法：電流是正電荷移動所造成的。

對於這樣的問題，我們只需要用靜電的手法就可以解決，你也許會好奇，電荷不是在移動嗎？這樣還能叫做靜電？這其實是翻譯上的問題，我們所稱的靜電，實際上是指達到穩態的電磁現象，像是一根穩定的載流導線，或是一個等速運動的帶電物體，至於電動力學的範疇，則往往牽涉到電磁交互產生的現象，我們不會多做討論。

圖一、電子在導線中移動的示意圖。（臺大物理系教授陳義裕繪）

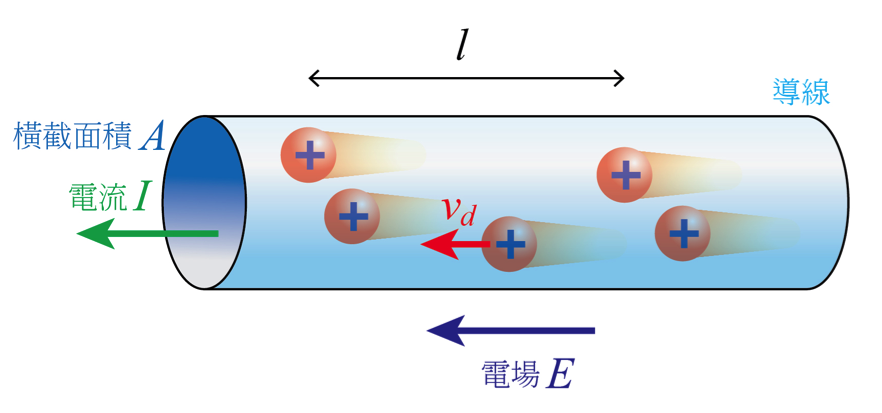
自從法拉第用電力線的概念表達庫倫定律後，大家慢慢的改用流體的觀點去解釋電流的行為，因此我們在國高中時就會聽到一個定義，電流就是某個截面積上單位時間內通過的電量。接下來的討論我們要延續這個觀點，但是要讓大家更有能力想像，所謂的漂移速度，是指電子在導線中移動的速度（圖一），且我們可以從國中的定義出發，做一個非常簡單的計算，你將會得到一個非常不敢相信的結果：

電流 $$\displaystyle I=\frac{q}{t}=\frac{nAle}{l/v_d}=nAev_d$$

其中 $$n$$ 是單位體積內帶有的電荷數，$$e$$ 是電子的電量，$$A$$ 是導線的橫截面積，$$l$$ 是一段長度，$$v_d$$ 就是漂移速度。這公式本身並不複雜，於是你移項完可以得到 ，那麼我們就可以去算算你打開家裡的電燈開關到它發亮需要多久的時間了：

一般的導線都是銅線，只要稍查資料就可以得到，銅的原子量是 $$6.355\times 10^{-2}~kg/mol$$，密度是 $$8.96~g/cm^3=8.96\times 10^3~kg/m^3$$，於是兩者相除就可以到單位體積內該有多少銅原子了，而又一個銅原子會釋放一個電子來導電，因此這個數字也就等於單位體積內的自由電子數 $$n=\frac{8.96\times 10^3~kg/m^3}{6.355\times 10^{-2}~kg/mol}=1.41\times 10^5\times 6.02\times 10^{23}~(1/m^3)$$，

然後假設電流大小是 0.55 安培（一般家用電壓是 110V，燈泡功率約 60W），而導線的截面積約是 $$A=10^{-6}$$，於是代入剛剛的式子中，就可以得到漂移速度 $$v_d=\frac{0.55}{1.41\times 10^5\times 6.02\times 10^{23}\times 10^{-6}\times 1.6\times 10^{-19}}\approx 4.0\times 10^{-5}$$，也就是每秒大約四毫米左右。如果你家電燈架在三公尺高的天花板上，用這種速度傳送訊號的話看起來實在太沒有效率可言了，而且似乎和生活經驗違背了。那麼到底這其中有著什麼樣的玄機呢？

我們再一次用流體的例子去解釋這件事情，我們很輕易便能接受一根銅線拿來就有許多電子已經在其中準備好要移動了，我們可將這件事情看做是一根水管裝滿了水，隨時準備澆花，當我們打開水龍頭，裝滿水的水管馬上有水從管口噴出，這時如果我問你第一波噴出來的水跟水龍頭的水是同一個嗎？你會馬上回答我不是，於是你就想通讓電燈亮起來的電流也不是從開關這裡出發慢慢走到電燈的，不過這個發亮的動作一定還是從開關發號施令的，意味著某種東西告訴燈泡端要有動作，而那個東西不偏不倚就是電磁波。雖然電磁波在導線上傳遞的速率不會那麼理想幾乎等於光速，但是以 SI 制來度量，速率的數量級仍然在十的八次方左右，遠遠超過電子自身的漂移速率。

那麼你現在明白國高中的老師們是懷著怎麼樣的心情在用水管跟你比喻導線的了，只不過他們也許無法完整的交代好場的概念，但那依然不影響我們了解漂移速率所代表的真正意義。

參考文獻

1. Ohm’s law and drift velocity in conductors — Physclips: Mechanics with animations and film. http://www.animations.physics.unsw.edu.au/jw/drift.html
2. 周深淵。第5章 電流。電磁學。虎尾科技大學。     http://140.130.15.232/student/file/%E9%9B%BB%E7%A3%81%E5%AD%B8/05%E9%9B%BB%E6%B5%81.pdf