【物理世界】量子霍爾效應(四):迪拉克複合費米子
【物理世界】量子霍爾效應(四):迪拉克複合費米子
蕭維翰
這兩年物理學家提出了新的粒子電動對稱的理論解釋最低蘭道階(Landau Level)的物理,此新模型不再透過將磁通量附著到原粒子身上,而是藉由粒子漩渦對偶性,用更自然的方法去闡述一些實驗上觀測到的現象。
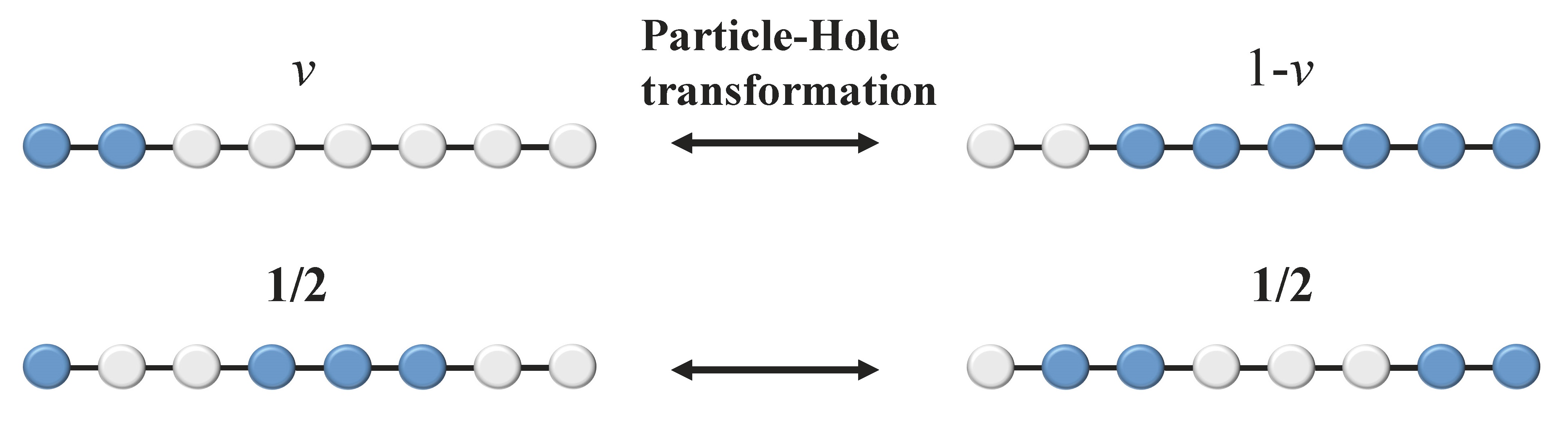
在前面幾篇文章中,我們介紹了量子霍爾效應的現象,並為分數與整數量子效應提供一些解釋。再者我們討論了 Jain 的複合費米子理論,指出實驗上觀測到的分數 \(\frac{1}{3},~\frac{2}{5},~\frac{3}{7},…\) 或 \(\frac{2}{3},~\frac{3}{5},…\) 等,都能被 Jain 序列所說明。在結尾處,我們指出 Jain 序列的極限是 \(\frac{1}{2}\),在那個狀況下,複合費米子看不到磁場,並形成一個費米液體。針對這個問題, HLR 是一個知名的有效理論。