Hubbard 模型（四）：費米 Hubbard 模型：簡單的解析事實（下）
蕭維翰
緊接著上文，我們在此介紹費米 Hubbard 模型中怎麼產生鐵磁性。
圖一
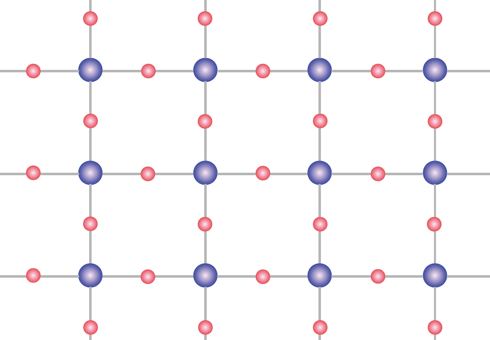
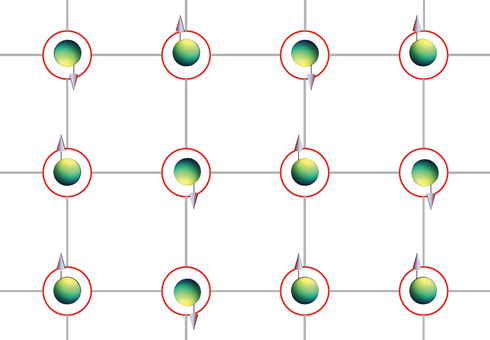
在前文中我們定義了費米 Hubbard 模型，並花了一點空間討論當躍遷常數 t 與交互作用 U 都不為零，但後者遠大於前者的時候，透過一個二階的量子過程，半填滿的晶格在能量上會偏好相鄰的兩個費米子擁有反向的自旋，這構成了「反鐵磁性」（antiferromagnetism）的可能性。
事實上，這個物理直覺約略是正確了，但僅僅兩個節點，一般而言不太能給我們精確的「物質相」預測，因為後者往往是定義在熱力學極限（thermodynamic limit），意指在系統自由度趨近無限大的時候。
Hubbard 模型（三）：費米 Hubbard 模型：簡單的解析事實（上）
蕭維翰
我們首先介紹在費米 Hubbard 模型中一些可由直覺跟解析解理解的事實。
Figure1. （photo credit: 作者自繪） 由於不相容原理，當系統沒有躍遷能力的時候，費米 Hubbard 模型最低能量的組合便是盡可能地讓每個粒子都佔有一個晶格點。
經歷了前面兩篇暖身，有忍住讀完的讀者們應該稍微對 Hubbard 模型有了基本的了解。本文中我們繼續考慮類似的模型，但在這裡我們把粒子們換成費米子。
費米子與玻色子的根本差異在於前者遵守庖立不相容原理（Pauli Exclusion Principle），一個系統內不會有兩個具有一模一樣量子數的費米子，這也將大大的影響我們對基態物質相的分析。
Hubbard 模型（ㄧ）：動機與定義
蕭維翰
我們將利用一個系列文跟大家介紹一個在凝態物理中很重要的模型家族。
前兩篇文章跟讀者定性地講述了在討論金屬性質時，大家所謂的典範式的蘭道理論是什麼意思。筆者預計再花至少一兩篇文章聊聊現在當紅的「怪金屬」（Strange metal）和「壞金屬」（bad metal），探討它們與正常金屬的差異，並盡筆者能力所及跟大家說明背後的原因。
v=v=5/2 量子霍爾態之謎（中）
蕭維翰
誰是描述v=5/2基態的波函數？曾經我們都快要相信就是 Pfaffian 波函數，直到 …… 。
Figure1. 2+1 維流體中可能的漩渦組態。（photo credit: 作者自繪）
誰是描述v=5/2基態的波函數？曾經我們都快要相信就是 Pfaffian 波函數，直到 …… 。
在前文中我們複習了量子霍爾效應，並在文章的下半段介紹 \(\frac{5}{2}\) 態，並說明為什麼他是個有趣的問題，並且用一個問題結尾 —— 我們有沒有一個類似 Laughlin 波函數的試驗波函數來代表這個狀態。而在本文中我們將更深入地討論這個懸問。
在這之前，筆者想先釐清前文的一段敘述。
物理學中的對偶性(下)
蕭維翰
連結：物理學中的對偶性(上)
對偶性不只存在在前面的簡單例子中，其實我們也有費米子與玻色子、玻色子與玻色子、乃至於費米子與費米子間的對偶性。
圖一：水波中的孤波（photo credit: Wikipedia）
在上集的討論中，我們約略介紹了「對偶」（duality）在物理學中，的意思：表面上看起來不同的兩個理論，本質上提供一樣的描述。最基本的例子是所謂伊辛模型（Ising model）在原晶格與對偶晶格上的對偶，以及電磁學馬克斯威方程式（Maxwell equations）在沒有電荷下電場磁場交換的對偶性。
【物理世界】量子霍爾效應（四）：迪拉克複合費米子
蕭維翰
這兩年物理學家提出了新的粒子電動對稱的理論解釋最低蘭道階（Landau Level）的物理，此新模型不再透過將磁通量附著到原粒子身上，而是藉由粒子漩渦對偶性，用更自然的方法去闡述一些實驗上觀測到的現象。
圖一：在最低蘭道階中的粒子電洞轉換。\(\nu\) 填滿態會被轉換到 \(1-\nu\) 填滿態，而 \(\nu =\frac{1}{2}\) 擁有粒子電洞的對稱性。
在前面幾篇文章中，我們介紹了量子霍爾效應的現象，並為分數與整數量子效應提供一些解釋。再者我們討論了 Jain 的複合費米子理論，指出實驗上觀測到的分數 \(\frac{1}{3},~\frac{2}{5},~\frac{3}{7},…\) 或 \(\frac{2}{3},~\frac{3}{5},…\) 等，都能被 Jain 序列所說明。在結尾處，我們指出 Jain 序列的極限是 \(\frac{1}{2}\)，在那個狀況下，複合費米子看不到磁場，並形成一個費米液體。針對這個問題， HLR 是一個知名的有效理論。
【物理世界】量子霍爾效應（三）：複合費米子
蕭維翰
連結：【物理世界】量子霍爾效應（二）：分數量子化與 Laughlin 波函數
在 Laughlin 波函數後，J. Jain 提出了複合費米子的概念，將整數量子霍爾效應與分數量子霍爾效應結合在一個框架下，並成為研究量子霍爾效應的一個典範。
本圖引自1990年6月22《科學》雜誌封面，courtesy of illustration T. S. Duff and T. Kovacs, AT&T Bell Laboratories
儘管 Laughlin 波函數從定量的角度提供了當時人們了解某些分數霍爾態的出發點，它並不稱得上是一個完整的「故事」。另一方面，它的成功也多侷限於 \(\frac{1}{3},~\frac{1}{5}\) 等分數，而不涵蓋其他如 \(\frac{2}{5},~\frac{3}{7}\) 等也在實驗中被發現的狀態。
旋轉的玻色愛因斯坦凝聚態
蕭維翰
圖一：旋轉的 BEC 中的漩渦和真實的漩渦
高中的物理課程中，我們學習動量、角動量，用這兩個量來量化一個物件平動狀態以及轉動的狀態。儘管大多數人在大學後不會再接觸更進階的物理課程，但事實上就描述運動狀態而言，也沒有更多新的物件了。
物理學的理論描述是盡量得跟實驗呼應的，也因此，即便是今日大如強子對撞機的尖端實驗，源頭的想法也都是想藉由動量、角動量等在交互作用的前後關係，去獲得物理資訊。
本文就來略談，當我們轉動一個流體，更精確地說，一個玻色愛因斯坦凝聚態（Bose-Einstein Condensate），什麼事情會發生。
南部加法規則：希格斯粒子、NJL 模型、超流體氦與BCS超導體（下）
蕭維翰
連結：南部加法規則：希格斯粒子、NJL 模型、超流體氦與BCS超導體（上）
南部陽一郎（なんぶよういちろう）在研究 BCS 、NJL、與費米超流氦的質量光譜後，提出了模型中費米子質量與玻色子質量應該滿足的關係，這就是南部的加法規則。
在上文中我們花了一些篇幅複習關於超導體與希格斯物理的一些歷史，闡述了粒子物理學家南部陽一郎為何投入超導體問題的研究，並如何利用他在過程中所掌握的精髓反饋到核物理的研究，以超導體 BCS 模型為原型，提出 Nambu-Jona-Lasinio （NJL）模型。
玻色子與費米子二：粒子特性 (Bosons and fermions Ⅱ: Particles qualities)/strong>
國立臺灣大學物理系 林惟淨
在上一篇文章中我們解釋了玻色子與費米子的理論來源，是由我們必須改寫多粒子狀態下全同粒子的波函數而得。延續著玻色子與費米子的主題，接下來在這篇文章中，我們則要介紹這兩種粒子的特性。