和算家求橢圓周長的方法(二)(Wasan’s method of finding the formula of the circumference of an ellipse Ⅱ)
和算家求橢圓周長的方法(二)
(Wasan’s method of finding the formula of the circumference of an ellipse Ⅱ)
臺北市立和平高中教師黃俊瑋
如前文〈和算家求橢圓周長的方法(一)〉所述,和田寧是最早造出正確橢圓周長展開式的數學家,然而,他的主要著作皆在西元1836年的一場大火中付之一炬,因此,我們只得以他授予的弟子們的傳書,一窺他求解橢圓周長的方法。
和田寧的弟子小出兼政,依據和田寧所授之傳書編成《圓理算經》,該書〈上卷〉的第五部份裡,提出了求橢圓周長問題:「譬今有如圖橢圓,只言長徑若干,短徑若干,問得周長術如何?」作者造橢圓周長公式的過程中,主要是利用分割求和的積分方式,輔以各類「圓理表」。以下,筆者進一步說明並分析他求橢圓周長的過程。
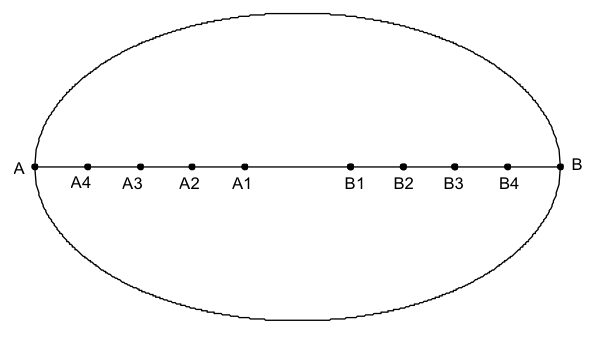
假設橢圓之長軸長為 \(2a\)、短軸長為 \(2b\),首先,小出兼政先利用「截弦順法對橢圓之長軸作分割,配對得到 \(n\) 段,讀者請參考圖一,以分割成配對 \(5\) 等分的情況為例作說明。此分割法是以左右配對 \(5\) 等分割的方式,對橢圓之長軸作分割,使其滿足:
\(\overline{{A_1}{B_1}}=\overline {{A_1}{A_2}}+\overline {{B_1}{B_2}}=\overline{{A_2}{A_3}}+\overline{{B_2}{B_3}}= \overline{{A_3}{A_4}}+\overline{{B_3}{B_4}}=\overline{{A_4}A}+\overline{{B_4}B}=\frac{{2a}}{5}\)
這和現代教科書中所用的等分割方式有所不同。