半平面

二元一次不等式(Two-Variable Inequalities)
臺北市立第一女子中學數學科蘇俊鴻老師

若 $$a,b,c$$ 為實數，且 $$a,b$$ 不同時為0，則稱 $$ax+by+c=0$$ 為二元一次方程式；

又因為它的圖形為一直線，也稱為直線方程式。

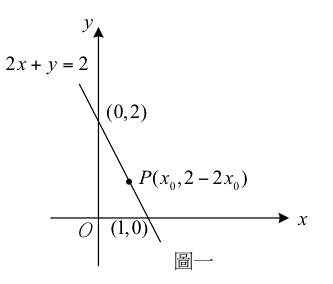
圖一正是二元一次方程式 $$2x+y=2$$ 的圖形。事實上，直線 $$2x+y=2$$ 上的任一點，

其坐標 $$(x,y)$$ 都滿足方程式 $$2x+y=2$$，換言之，都是方程式 $$2x+y=2$$ 的解。

因此，當點 $$P$$ 的 $$x$$ 坐標為 $$x_0$$ ，易推得 $$y$$ 坐標為 $$2-2x_0$$ 。