物理模擬影片五：理想氣體方程式的模擬
理想氣體方程式的模擬 (The Simulation on Ideal Gas Law)
國立臺灣大學物理學系石明豐教授
理想氣體
標準狀況下理想氣體與真實氣體間的熵值差－以SO2為例(二)
標準狀況下理想氣體與真實氣體間的熵值差－以SO2為例(二)
The entropy difference between the ideal gas and real gas under standard condition – a case study in SO2 (II)
國立臺灣師範大學化學系兼任教師 邱智宏
連結：標準狀況下理想氣體與真實氣體間的熵值差－以SO2為例(一)
二、伯特洛方程式和臨界點
欲求出不同氣態物質在伯特洛方程式中的 $$a$$、$$b$$ 數值，則需對此方程式稍作瞭解。現以水蒸氣為例，以壓力對莫耳體積作圖，在 $$200^\circ C$$ 時，會出現一段水平線(NLJ)，即體積減小壓力不變，此時開始有氣體凝結為液體，當溫度愈高時，水平的部分逐漸減短，到 $$374^\circ C$$ 時，水平線成為一點$$(C)$$，此點稱為臨界點( critical point )，此時液、氣間的界面消失，此點的溫度及壓力分別為臨界溫度$$(T_c)$$及臨界壓力$$(p_c)$$。
標準狀況下理想氣體與真實氣體間的熵值差－以SO2為例(一)
標準狀況下理想氣體與真實氣體間的熵值差－以SO2為例(一)
The entropy difference between the ideal gas and real gas under standard condition – a case study in SO2 (I)
國立臺灣師範大學化學系兼任教師 邱智宏
純物質的焓(enthalpy)、自由能(Gibbs free energy)及熵(entropy)是化學熱力學經常要使用到的數據，因此一般化學教科書均會將一些常見物質的相關數據，表列在附錄中，以供參考及使用。但是這些數據是如何求得的？卻鮮少被討論，尤其表列純物質的熵，若在標準狀態下為氣體，則其設定的情況為該氣體為理想氣體。
事實上理想氣體的標準莫耳相對熵$$(S^\circ_{m,id})$$和真實氣體的標準莫耳相對熵$$(S^\circ_{m,re})$$是不一樣的，它們之間的差距是多少？本文擬以 $$\mathrm{SO_2}$$ 為例，利用熱力學的公式，按部就班的推導它們之間的差異，除了讓學子利用所學，真正應用在解決問題上，也期盼學子能感受到在計算過程中數學所扮演的重要角色。
標準狀況下理想氣體與真實氣體間的焓值差－以C2H6為例 (二)
標準狀況下理想氣體與真實氣體間的焓值差－以C2H6為例 (二)
The enthalpy difference between the ideal gas and real gas under standard condition – a case study in C2H6 (II)
國立臺灣師範大學化學系兼任教師 邱智宏
連結：標準狀況下理想氣體與真實氣體間的焓值差－以C2H6為例 (一)
二、伯特洛方程式和臨界點
欲求出不同氣態物質在伯特洛方程式中的 $$a$$、$$b$$ 數值，則需對此方程式稍作瞭解。現以水蒸氣為例，以壓力對莫耳體積作圖，在 $$200^\circ C$$ 時，會出現一段水平線(NLJ)，即體積減小壓力不變，此時開始有氣體凝結為液體，
標準狀況下理想氣體與真實氣體間的焓值差－以C2H6為例 (一)
標準狀況下理想氣體與真實氣體間的焓值差－以C2H6為例 (一)
The enthalpy difference between the ideal gas and real gas under standard condition – a case study in C2H6 (I)
國立臺灣師範大學化學系兼任教師 邱智宏
熱力學的主要內容除了三大定律及相關公式外，最常被討論到就是一些狀態函數(state function)，而其中經常被使用到的數值，就是純物質的焓(enthalpy)、自由能(Gibbs free energy)及熵(entropy)，因此一般化學教科書均會將一些常見物質的相關數據，表列在附錄中，以供參考及使用。
理想氣體和凡得瓦爾氣體的比較－以二氧化碳為例
理想氣體和凡得瓦爾氣體的比較－以二氧化碳為例
(Comparison of ideal gas and van der Waals gases – a case study in carbon dioxide)
國立臺灣師範大學化學系兼任教師 邱智宏
初學物理化學 (physical chemistry) 時，理想氣體 (perfect gas) 如影隨形，無時不在，隨時出現在各個不同的章節。由於理想氣體假設其氣體粒子不具有體積、粒子間没有吸引力、彼此間的碰撞為彈性碰撞，因此其 \(p \cdot V \cdot T\) 間的關係，可以簡潔的以 \(pV=nRT\) 加以描述。
然而真實氣體究竟佔有體積，彼此具有吸引力，碰撞時也非彈性碰撞，因此其許多特性和理想氣體不一樣，例如低溫高壓下，真實氣體大大偏離理想氣體、能被液化、有特殊的臨界點 (critical point)⋯ 等。歷來許多科學家總希望由簡潔的理想氣體方程式出發，企圖能找到一個足以說明真實氣體的方程式，其中凡得瓦爾方程式 (van der Waals equation) 就是一個很好的例子，在數學上雖然稍微複雜一些，但卻能解釋很多真實氣體的現象。
本文試著比較二種方程式的異同，並由其相異之處，解釋為何凡得瓦爾方程式更能接近真實氣體的理由。另外，以二氧化碳為例，觀察其相圖的變化情形，並說明凡得瓦爾方程式可信及不足之處。
均分定理
均分定理(Equipartition theorem)
國立臺灣大學物理系博士後研究員 羅雅琳
所謂均分定理是指對於古典系統來說，在當系統處在絕對溫度T之熱平衡下，每個自由度所貢獻的能量權重相同。舉例來說：若欲考慮理想氣體的平均動能，我們可透過馬克士威-波茲曼統計，來得知氣體分子運動時的方均根速率為[1]
\(v=\displaystyle\sqrt{v_x^2+v_y^2+v_z^2}=\sqrt{\frac{3k_BT}{m}}\cdots(1)\)
，其中 \(m\) 為粒子的質量，而 \(k_B=1.38\times 10^{-23}\)(單位：焦耳/絕對溫度)是為了紀念波茲曼在物理上的貢獻，而用其名字來命名的波茲曼常數。
可逆與不可逆過程、絕熱與等溫膨脹的差別（下）
可逆與不可逆過程、絕熱與等溫膨脹的差別（下）
國立臺灣師範大學化學系兼任教師邱智宏
二、絕熱與等溫可逆膨脹
理想氣體在等溫可逆膨脹的情況，已如上述說明，現將上篇圖一的裝置及操作方式稍做修改，即容器並非浸入等溫槽，而是處於絕熱狀態，亦即系統和外界間没能熱量的交換$$(\mathrm{d}q = 0)$$，其餘的操作則完全相同，為一可逆過程。當膨脹開始時，系統對外作功，因為是絕熱狀態無法對環境吸熱，因此將造成內能減少$$(\mathrm{d}U = \mathrm{d}q + \mathrm{d}w)$$，系統的溫度因而下降，不再像等溫可逆膨脹時一樣，溫度為定值。
由公式的推導可知，理想氣體在等溫時 $$p_TV_T=$$定值(下標 $$T$$、$$a$$ 分別代表等溫及絕熱過程)，而在絕熱時，$$p_aV_a^\gamma=$$定值（請參考高瞻平台文章：定壓熱容量（Cp）和定容熱容量（Cv）的差別），其中 $$\gamma=C_p/C_V$$。
由於 $$\gamma$$ 大於 $$1$$，當二種過程從「相同」的起始點開始$$(p_TV_T=p_aV_a^\gamma=$$定值$$)$$，膨脹至相同體積時$$(V_T=V_a)$$，因為 $$V_a^\gamma>V_T$$，則絕熱系統的壓力下降比等溫系統多$$(p_T>p_a)$$，因此在圖二 $$pV$$ 相圖中，絕熱線下降的斜率比等溫線徙峭，而且如圖二所示，其結束點無法重合，必須再經過等容的加熱過程，絕熱膨脹方能再回到等溫膨脹過程的終點。
定壓熱容量（Cp）和定容熱容量（Cv）的差別（下）
定壓熱容量（Cp）和定容熱容量（Cv）的差別（下）
國立臺灣師範大學化學系兼任教師邱智宏
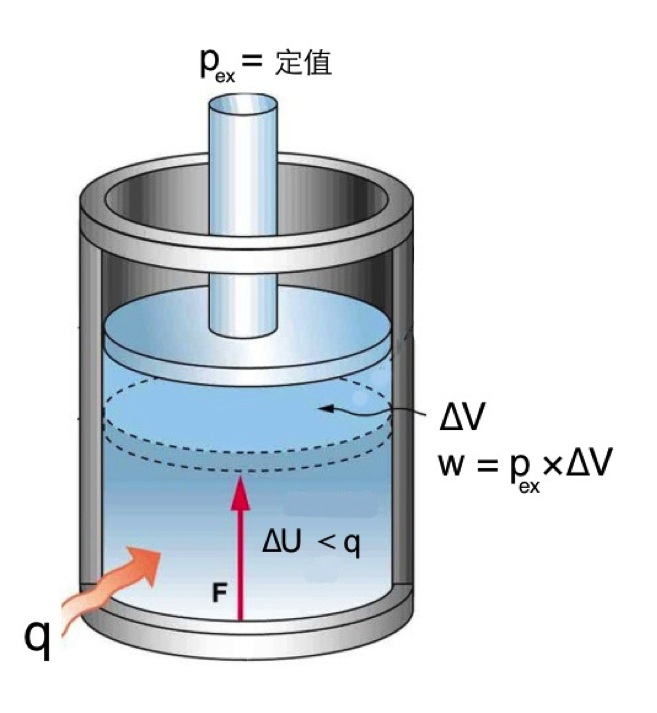
有了上篇 \(C_V\) 的測量基礎，為了更易於了解，我們先以氣體為例，若測定一定量氣體的 \(C_V\)，其升高 \(1~K\) 所需的內能變化\((\Delta U)\)，由於没有對外作功，其情況顯然和定壓下升高 \(1~K\)，焓的變化量\((\Delta H)\)有所不同，如圖二所示：當系統在等壓情況下，吸收定量的熱時，除了系統的內能會增加，系統內的溫度因而上升，使容器內壓力加大向上膨脹，對外作功，直至內壓等於外壓\((p_{ex})\)時停止。此時系統對外做功\((w=p_{ex}\times \Delta V)\)，因此系統吸收的總熱量\((q)\)，有一部分要用來對外作功，所以系統增加的內能\((\Delta U)\)將小於 \(q\)。
據此，等量的物質，在定壓下系統上升 \(1~K\)，所吸收的熱量\((q_p)\)，要比在定容下上升 \(1~K\) 所需的熱量\((q_c)\)還要多，因此在氣態的物質中，\(C_p\) 恒大於 \(C_V\)。
圖二\(~~~\)定壓下加熱系統，由於物質體積膨脹 \(\Delta V\)，系統需對外作功\((w)\)，其定壓之熱容量大於定容的熱容量。
理想氣體方程式
理想氣體方程式 (Ideal gas law)
臺中縣縣立中港高級中學物理科王尊信老師/國立彰化師範大學物理系洪連輝教授責任編輯
所謂理想氣體方程式是指理想氣體的壓力 \((P)\)、體積 \((V)\)、莫爾數 \((n)\) 與絕對溫度 \((T)\) 的關係滿足 \(PV=nRT\) 的簡單關係式，其中，\(R\) 為理想氣體常數 \(=0.082~\text{atm-L/mole-K}\) 或 \(8.31~\text{J/mole-K}\)。理想氣體方程式是根據波以爾定律(Boyle’s law)與查理定律(Charles’s law)結合而來。
理想氣體與真實氣體的差別，在於理想氣體不考慮氣體分子本身所佔的體積，只考慮氣體分子運動的體積。因為氣體本身所佔的體積並不考慮，所以理想氣體分子間的相互作用力也不考慮。相對地，對於真實氣體而言，氣體分子間相互作用力不可忽略，稱為凡德瓦力(Van der Waals force)。因為上述的種種性質，當真實氣體的凡德瓦力較小時，比較接近理想氣體，因此在高溫與低壓時，真實氣體接近理想氣體，比較接近理想氣體方程式的規範。
Pages
- 1
- 2