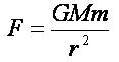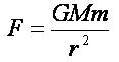我猜牛頓是這樣得到第三運動定律
行政院科技部科技顧問／瑞典林雪平大學榮譽教授 趙光安
我在高雄中學高中三年級的物理課是從力學開始：牛頓萬有引力定律，牛頓的三個運動定律，虎克定律，… 等等。我曾經自創一個“表面粗糙模型”，應用牛頓第二運動定律，推導出來虎克定律，於是更想知道牛頓是如何發現這些重要定律。雖然我是茫無頭緒，我的物理老師胡宇平也不能給我答案，他卻鼓勵我不要放棄。
過去幾十年中，斷斷續續的偶爾想到這回事。來到歐洲以後，得利於天時、地利、人和，終於摸索出一些頭緒。
從牛頓的時代背景探索第二運動定律（上）
行政院科技部科技顧問／瑞典林雪平大學榮譽教授 趙光安
牛頓的萬有引力定律及三條運動定律，都和「力」關係密切。因此，如果我們要討論牛頓創立的古典力學，應該先釐清，在牛頓之前，「力」的觀念是什麼？到了牛頓的時代，「力」的定義又是什麼？如果不明白「力」的定義，我們還是可以機械式的把牛頓力學「應用」到各類問題上，但是很難「認識」牛頓力學的根源。
從牛頓的時代背景探索第二運動定律（下）
行政院科技部科技顧問／瑞典林雪平大學榮譽教授 趙光安
在伽利略和牛頓的時代，數學工具只有幾何、三角、和代數，物理知識也僅限日常生活中有系統的觀察，及少數的實驗結果。用現代的標準來衡量，伽利略和牛頓頂多只有國中畢業的程度。如果我們用現代的數理常識背景來解答三、四百年前的問題，那就是「事後有先見之明」了。雖然和「力學」有關的量測，伽利略得到的數據被推崇是權威性，然而他的「力學」實驗幾乎全部是基於物體的直線運動。在這個時代背景下，牛頓建立的理論，是從「一維系統」開始，然後才推廣到「三維空間」。因此，我們也從直線運動開始，試試看能否經歷一趟牛頓的思路。
由問題的起源看導數的定義II
臺北市立西松高中 蘇惠玉教師
在前一篇文章中，我們已經看過費馬求極值的方法了，也就是當 \(e\) 是個很微小的量時（亦即趨近於 \(0\)），讓 \(\frac{f(a+e)-f(a)}{e}\) 這個值「盡可能的逼近」\(0\)。
接下來我們來看看牛頓求切線的方法。
牛頓求切線的方法
下面的方法出現在牛頓的《曲線求積術》，撰寫於 1693 年，並於 1704 年作為《光學》一書的附錄正式發表。牛頓以求切線的策略與方法，說明他的「流數方法（即求導數的方法）」，並舉函數為 \(y=x^n\) 為例，實際演練操作他的方法。
牛頓 (Isaac Newton)
國立彰化師範大學物理學系研究所楊婕妤研究生/國立彰化師範大學物理系洪連輝教授責任編輯
牛頓(1643-1727) 是人類史上最偉大的物理學家之一，他創立了微積分，發現白光被稜鏡散色的光譜，陳述著名的「力學三大運動定律」、及「萬有引力定律」。為了紀念他的偉大發現，力的單位就用「牛頓」來命名。
牛頓於1643年12月25日於英國林肯郡鄉下的一個小村落誕生，然而在他出生前父親就去世了，他是個早產兒所以身材比一般小孩嬌小虛弱，兩歲那年母親改 嫁給一位名為史密斯的牧師，母親將他託付給外祖母照顧。牛頓開始在鄉村學校學習，他只喜歡數學，所以小時候成績並不好，可是他很喜歡動手做實驗，對於自然 現象極感興趣！可是老師很瞧不起他，後來勤奮向學，終於在班上名列前矛。
15歲時繼父過世，母親要牛頓休學管理農事，牛頓卻熱衷於設計機械與研究數學，之 後在舅舅及國中校長鼓吹下，母親終於同意牛頓繼續他的學業。18歲那年他進入劍橋大學三一學院學習，在那裡他遇到了學業啟蒙導師-巴羅老師，教導地理、物 理、天文和數學等，他注意到牛頓的自然科學及數學方面的優異理解能力，1665年牛頓發現了二項試定理，那年他也得到學士學位。
牛頓第一運動定律 (Newton’s first laws of motion)-2
基隆市立暖暖高級中學物理科張志康老師/國立彰化師範大學洪連輝教授責任編輯
「牛頓第一運動定律」是牛頓在「自然哲學的數學原理(牛頓，1687)」一書中所提出的一則定律。此定律奠基於伽利略及牛頓等人的實驗與理論而建立，伽利略認為：「力並不是物體『維持運動狀態』的必要條件，而是『改變物體運動狀態』的必要條件」。對此，牛頓近一步解釋：「所謂的『運動狀態』，指的是物體的動量」。
牛頓第一運動定律 (Newton’s First Laws of Motion)-1
臺北市立第一女子高級中學物理科張清俊老師/國立彰化師範大學洪連輝教授責任編輯
牛頓運動定律是古典物理的基礎，用來描述物體受力和運動間的關聯，其中第一定律又稱為慣性定律，定律內容描述當物體不受外力或外力和為零時，物體會維持原本的運動狀態，亦即靜者恆靜、動者恆做等速度運動。
