貝葉斯和貝氏定理(3)（Thomas Bayes and Bayes’ Theorem (3)）
臺北市立第一女子高級中學蘇俊鴻老師
連結：貝葉斯和貝氏定理(2)
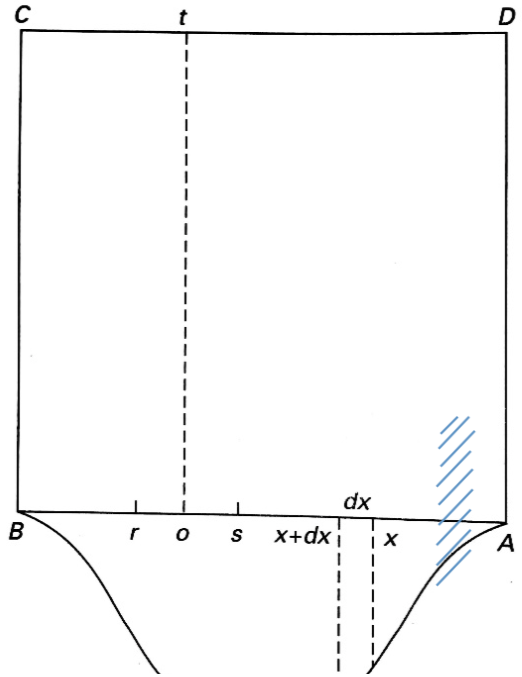
接著，我們來看貝葉斯如何求出 \(P(F)\) 和 \(P(E\cap F)\)。他用了一個頗為獨特的想法，據以建立機率模型進行計算。如圖一，考慮水平擺放一個正方形的桌面或平面 \(ABCD\)，將球 \(O\) 或 \(W\) 拋向桌面，並假設它們落在桌面上任何相等區域內的機率相同。
這時，假設球 \(W\) 先拋，過落點畫一條直線 \(ot\) 平行 \(AD\)，分別交 \(CD\) 與 \(AB\) 於 \(t\) 和 \(o\)。接著，球 \(O\) 被拋擲 \(p+q=n\) 次，如果它一次單獨拋擲中落在 \(AD\) 和 \(ot\) 之間，稱為在一次試驗中發生了事件 \(M\)。
圖一
貝葉斯和貝氏定理(1)（Thomas Bayes and Bayes’ Theorem (1)）
臺北市立第一女子高級中學蘇俊鴻老師
貝氏定理(Bayes’ Theorem)在高中數學的機率單元中出現，被當成是條件機率的重要議題，為人所知的是它的定理內容：
設 \(\left\{ {{A_1},{A_2}, \cdots ,{A_n}} \right\}\) 為樣本空間 \(S\) 的一組分割，\(B\) 為 \(S\) 的任一個事件，
若 \(P(B)>0\)，則在事件 \(B\) 發生的情況下，事件 \(A_k\) 發生的機率為
\(\displaystyle P\left( {{A_k}|B} \right) = \frac{{P\left( {{A_k}} \right)P\left( {B\left| {{A_k}} \right.} \right)}}{{\sum\limits_{i = 1}^n {P\left( {{A_i}} \right)P\left( {B\left| {{A_i}} \right.} \right)} }},1\le k\le n\)
以及課本提及的應用，如品管檢驗、醫學檢定等。但多數人不知道貝氏是誰？什麼問題促使他發展出貝氏定理？貝氏定理在現今統計學上有著廣泛的應用，但學說提出之初，就如此為數學家和統計學家所擁護嗎？這些問題都是本文撰寫的動機。首先，就由托馬斯．貝葉斯(Thomas Bayes, 1702-1761)的生平開始說起，貝氏定理正是由他所提出的。
巴斯卡其人其事(II)（The biography of Blaise Pascal, part 2）
臺北市立西松高中蘇惠玉教師
連結：巴斯卡其人其事(I)（The biography of Blaise Pascal, part 1）
1652年前後，法國貴族安東尼‧哥保德‧迪‧默勒爵士（Antoine Gombaud, Chevalier de Méré , 1607 – 1684）寫信給巴斯卡，提出了兩個問題：
巴斯卡除了自己研究解決方法之外，還寫信和費馬（Pierre de Fermat, 1601 – 1665）交流解法，在1654年他寫給費馬的一封信中寫道：
我和您的急切心情是一樣的，雖然還臥病在床，但抑制不住要告訴您，我昨天晚上從卡爾卡維手裡接到您關於點數問題的來信，我簡直不知道用什麼語言稱讚這封信。…
您的方法是正確的，而且是我所知道的這類問題研究中的首次正確答案。但由於在組合方面會遇到過多的麻煩，我找到另外一種更加簡潔的方法，…
巴斯卡其人其事(I)（The biography of Blaise Pascal, part 1）
臺北市立西松高中蘇惠玉教師
布萊思‧巴斯卡（Blaise Pascal, 1623-1662），出生於法國克萊蒙費朗（Clermont-Ferrand），對數學、物理、神學宗教都有深入的研究與貢獻。他三歲喪母，是家中的獨子，八歲時舉家搬到巴黎。他的父親對教育擁有與眾不同的觀點，決定親自教養他的小孩，並且為了避免影響到布萊思對拉丁文與希臘文的學習，在他15歲前禁止他學習數學並收起布萊思身邊所有與數學相關的著作。然而，這個從小天資聰穎的小孩，在他12歲時，居然獨自發現了三角形內角和等於二個直角的性質，於是他父親給了他著名的幾何學聖經《幾何原本（The Elements）》，決定讓他學習歐基里得的幾何學。
14歲時，他陪著父親開始參加梅森神父（M. Mersenne）的聚會。在17世紀的前半，梅森神父是當時世界的科學與數學集散中心，因此小巴斯卡得以在聚會中認識許多科學界與數學界的大咖級人物，包括在射影幾何上影響他甚深的狄沙格（Girard Desargues, 1591–1661）、笛卡兒（René Descartes, 1596 – 1650）以及法蘭西學院的數學教授羅伯沃（Gilles Personne de Roberval, 1602 – 1675）。16歲時巴斯卡在狄沙格思想的影響下，認真創作了一份有關圓錐曲線的論文，裡頭包含了許多射影幾何的定理，還包括了著名的巴斯卡神秘六邊形，那是一個六邊形內接在圓錐內，它的各組對邊的交點共線。巴斯卡這份作品已相當具有成熟度，以致於笛卡兒看到這份手稿後拒絕相信它出自於一個16歲的少年之手。
馬可夫生平簡介(2)（A Brief Introduction of Markov’s Life: Part 2）
國立臺南第一高級中學數學科林倉億老師
連結：馬可夫生平簡介(1)
1905 年馬可夫退休後，他持續機率理論的研究，並開始專注在後來被稱為「馬可夫鏈 (Markov chain)」的問題上。當時馬可夫努力想要建立適用於一般情況下的機率極限法則，並同時推展某些理論的應用。
1906 年，馬可夫提交一篇論文〈大數法則在相依變數上的推廣〉(The Extension of the Law of Large Numbers on Mutually Dependent Variables)，後人所稱的「馬可夫鏈」或是「馬可夫矩陣」，就是首次出現在這篇論文之中。此後，馬可夫陸續發表幾篇有關這主題的論文，不但得到各種一般化的結果，也導出在某些條件限制之下，中央極限定理是成立的。
馬可夫生平簡介(1)（A Brief Introduction of Markov’s Life: Part 1）
國立臺南第一高級中學數學科林倉億老師
馬可夫 (Andrei Andreevich Markov, 1856~1922)在高中時就展露數學上的天賦與興趣，寫了他生平第一篇數學論文。雖然這篇論文並不是新的創見，但已經深深吸引到兩位聖彼得堡大學的數學教授科爾金 (Aleksandr Korkin, 1837~1908)與佐洛塔瑞夫 (Yegor Ivanovich Zolotarev, 1847~1878)的目光，後來馬可夫不僅進入聖彼得堡大學就讀 (1874年)，還參加了這兩位教授專為優秀學生開設的研討班。
ICMI的第一任主席克萊因（Felix Klein: The first president of International Commission on Mathematics Instruction, ICMI）
國立臺灣師範大學數學系洪萬生教授/國立臺灣師範大學數學系洪萬生教授責任編輯
所謂的 ICMI 是國際數學教育組織，每四年召開一次全球性的國際數學教育會議（International Congress on Mathematics Education, ICME）。明年（2012年），此一國際研討會將在南韓召開，是國際數學教育界的一大盛事。
這個組織的第一任主席，就是偉大的德國數學家克萊因（Felix Klein, 1849-1925）。他出任的原因之一，當然有可能是因為他長期關心數學教育，因此，他以大數學家之尊「蹲下去」，應該在國際之間發揮了極大的影響力吧。
阿拉伯的數學（Arabic Mathematics）
國立臺灣師範大學數學系洪萬生教授/國立臺灣師範大學數學系洪萬生教授責任編輯
在人類歷史中，阿拉伯人的數學發展，正如其他文明一樣，有其獨特的一面。不過，由於回教與基督教的長期衝突，使得由西方學者所主導的數學史研究中，對於阿拉伯數學始終很少給出應有的肯定與評價。因此，我們特別在此高瞻計畫中，簡介阿拉伯數學的成就及意義。希望經由此一文明窗口，讓我們一起欣賞異文化的數學意義與價值。
如何閱讀祖沖之？（How to Read Zu Chongzhi?）
國立臺灣師範大學數學系洪萬生教授/國立臺灣師範大學數學系洪萬生教授責任編輯
對於很多人來說，祖沖之並不是陌生的中國歷史人物，譬如說吧，在一些中國古代科學家的傳記書寫中，都一定可以找到他的故事，完全不需要我們在此狗尾續貂。
不過，敘說他的生平事蹟，並著重與他的數學成就比較相關的部份，乃至於他如何看待他自己的貢獻，從傳記書寫與閱讀的觀點來看，似乎還是值得一說再說。在此，我們打算「重建」有關他的歷史故事。其中，還要特別說明有關圓周率近似值「祖率」$$\frac{355}{113}$$（日本數學史家三上義夫所命名）之價值與意義。