二次曲線 | 科學Online

橢圓平行弦中點共線問題（Collinearity Problem on the Midpoints of Parallel Chords of an Ellipse）

2014/09/25

橢圓平行弦中點共線問題
（Collinearity Problem on the Midpoints of Parallel Chords of an Ellipse）
臺北市立和平高中黃俊瑋教師

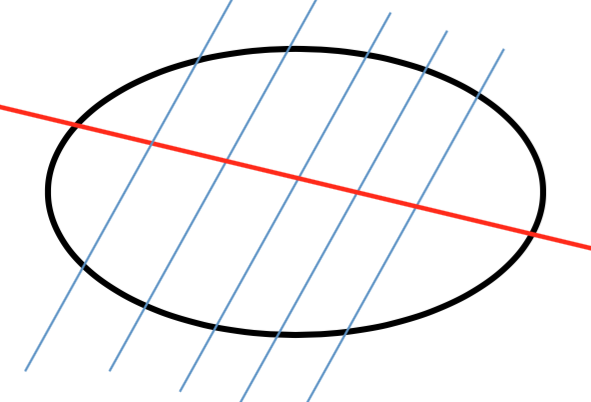
高中圓錐曲線單元裡，一個常見的延伸問題如下：在橢圓 $\Gamma :\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1$ 內所有斜率為 $2$ 的平行弦，已知這些弦的中點共線，請問其所在直線方程式為何（參見圖一）？

換言之，本問題相當於：已知直線 $y = 2x + k$ 與 $\Gamma :\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1$ 相截於兩點 $A,B$，當參數 $k$ 變動時，求 $A$ 與 $B$ 之中點 $M(x,y)$ 的軌跡所在直線方程式。

圖一$~~~$斜率為 $m$ 的平行弦中點軌跡所在圖形

繼續閱讀→

Dandelin Spheres證明圓錐截痕的焦點性質

2013/10/30

尚無留言

Dandelin Spheres證明圓錐截痕的焦點性質
臺北市立西松高中數學科蘇惠玉老師

目前實施的99課綱高中數學中，弱化了圓錐曲線的單元，所謂的「圓錐截痕」不再是必須教授的單元。各版本課本或數學教師在教授時也僅是簡單的陳述平面與圓錐的截痕何時為圓、橢圓、拋物線或雙曲線，基本上與課本採用的焦點定義方式無法連結，學生只是被動地接受老師所說的與模型所看到的曲線名稱而已。

不過，藉由 Dandelin 球面的想法，我們可將圓錐截痕與焦點的定義方式連結，以一種較為簡潔的形式，證明阿波羅尼斯在《錐線論》中所陳述與證明的性質。

繼續閱讀→

Steiner 圓系知多少(On Steiner Chain)

2011/09/09

尚無留言

Steiner 圓系知多少(On Steiner Chain)
國立臺灣師範大學數學系趙文敏教授/國立臺灣師範大學數學系趙文敏教授責任編輯

摘要:本文介紹Steiner圓的一些性質。

給定平面上一對內離圓 $$O_1(r_1)$$ 與 $$O_2(r_2)$$，其中圓 $$O_2(r_2)$$ 位於圓 $$O_1(r_1)$$的內部。

若 $$\{C_k\}_{k=1}^n$$ 是滿足下述四個條件的有限多個圓，則 $$\{C_k\}_{k=1}^n$$ 稱為是與內離圓 $$O_1(r_1)$$、$$O_2(r_2)$$ 相切的一組Steiner 圓系 ( Steiner chain )：

繼續閱讀→

恆寬曲線（Curve of Constant Width）

2011/08/17

尚無留言

恆寬曲線（Curve of Constant Width）
台北市立大直高級中學數學科高子婷老師/國立台灣大學數學系翁秉仁教授責任編輯

摘要：本篇文章從「恆寬曲線」談起，最後回到圓的定義，藉由恆寬與圓的差別體會圓的精妙。

何謂恆寬曲線

工程上稱某種曲線為「恆寬（constant width）曲線」：平面上一凸形封閉曲線，不論如何轉動，其寬度永遠不變，則稱之。所謂「寬度」是指平行線夾住某封閉曲線時，平行線間的距離即是。簡單說來，若以恆寬曲線作為輪子，並在其上放置板子，則乘客於上頭並不會顛簸；反之，若其非恆寬曲線，則當輪子轉動時板子間的寬度就改變了，乘客想必非常暈眩；舉例來說若用梯形當輪子，因為一轉動板子間的寬度就變了，所以梯形不是恆寬曲線。

繼續閱讀→